EEM.ssr:  Tutorial solutions

1. Give a definition of automatic speech recognition that distinguishes it from other speech technologies.
   ASR converts spoken words to text, whereas spoken language understanding includes machine reading comprehension, for example.
2. How can speech technologies be said to increase access of people with disabilities to computer-based systems?
   As a method for converting natural language from one modality (auditory) into another (visual), ASR can form part of a more flexible human-computer interface, especially for those with limited auditory function. Equally, speech synthesis (i.e., TTS) can help the blind or visually impaired access information stored on computer or the internet by vocalising text. Speech recognition can be used to assist those unable to type, e.g., through disability or injury, with text input. Speech synthesis can provide a voice where the user cannot speak. Sometimes providing an interface that combines modalities can be of benefit to people with learning difficulties or special needs of various descriptions.

3. What acronym denotes the convention for transcribing the sounds of the world's languages?
   IPA, International Phonetic Alphabet.
4. What is the difference between phones and phonemes?
   A phoneme is an abstract sound category within a language, whereas a phone denotes a practical realisation by a given speaker in a particular context.
5. What three attributes of natural speech contribute most to the non-linguistic aspects known as prosody?
   (i) intensity or amplitude, (ii) timing or duration, and (iii) pitch or intonation.

6. How can a basic understanding of phonetics facilitate the study of speech signals?
   It informs us of the sounds of a language and their categorisation.
7. What is a diphthong? Illustrate your answer with an example.
   A transition from one vowel sound to another, e.g., as in "by", "boy" and "bough".
8. What class of sounds includes /m/, /n/ and /ng/?
   Nasals are all produced with an occlusion of the vocal tract in the oral cavity.
9. What characteristics of the acoustic signal are most useful for discriminating vowels?
   The first two formant frequencies, F1 and F2.
10. Give three environmental factors that can affect the way speech is produced.
    Noise (Lombard effect), vibration, stress/fear, cognitive loading, fatigue, gas properties (air pressure/helium), etc.
11. What are the three places of articulation for English plosive consonants (aka. stops )?
    Labial (at the lips), alveolar (at the palatal ridge toward the front of the mouth), and velar (on the soft palate further back in the mouth).
12. What is the main difference between the way that the sounds /t/ and /s/ are produced?
    /t/ is a plosive consonant which has a transient burst when air is suddenly released; /s/ is a fricative consonant which is produced by turbulent flow and can be sustained. However, they are both produced at approximately the same place of articulation.
13. What name is given to the effect in fluent speech where, for example, the phrase ``isn't it'' is pronounced as if it were ``in'it''?
    Elision, just like "bread and butter" becoming "brembudder".

Dynamic Time Warping:

1. Write a pseudocode description of the DTW algorithm using the transitions shown in Fig.1 (left). Apply a distortion penalty for the horizontal (H) and steepest (S) transitions, d_H = d_S = d_μ/4, where d_μ denotes the mean distance found across the training data.
   

   1. Initially:	D(1,i) =	{ d(1,i) { 0	for i=1 otherwise (2,...,N)
   2. For t=2,...,T:	D(t,i) =	{ d(t,i) + D(t-1,i)+dH { d(t,i) + min[ D(t-1,i)+dH, D(t-1,i-1) ] { d(t,i) + min[ D(t-1,i)+dH, D(t-1,i-1), D(t-1,i-2)+dS ]	for i=1 for i=2 otherwise (3,...,N)
   3. Finally:	Δ =	D(T,N)

   
    
2. Modify your pseudocode to disallow two consecutive horizontal transitions, as shown in Fig.1 (right).
   

   1. Initially:	D(1,i) =	{ d(1,i) { 0	for i=1 otherwise (2,...,N)
   	isFlat(i) =	FALSE	for i=1,...,N
   2a. For t=2:	D(t,i) =	{ d(t,i) + D(t-1,i)+dH { d(t,i) + min[ D(t-1,i)+dH, D(t-1,i-1) ] { d(t,i) + min[ D(t-1,i)+dH, D(t-1,i-1), D(t-1,i-2)+dS ]	for i=1 for i=2 otherwise (3,...,N)
   	isFlat(i) =	{ TRUE { FALSE if arg min == D(t-1,i)+dH otherwise	for i=1,...,N
   2b. For t=3,...,T:	if isFlat(i) == TRUE
   		D(t,i) = { INFINITY { d(t,i) + D(t-1,i-1) { d(t,i) + min[ D(t-1,i-1), D(t-1,i-2)+dS ]              for i=1 for i=2 otherwise (3,...,N) isFlat(i) = FALSE for i=1,...,N
   	else
   		D(t,i) = { d(t,i) + D(t-1,i)+dH { d(t,i) + min[ D(t-1,i)+dH, D(t-1,i-1) ] { d(t,i) + min[ D(t-1,i)+dH, D(t-1,i-1), D(t-1,i-2)+dS ] for i=1 for i=2 otherwise (3,...,N) isFlat(i) = { TRUE { FALSE if arg min == D(t-1,i)+dH otherwise for i=1,...,N
   	end
   3. Finally:	Δ =	D(T,N)

   
    
3. How can silence and wildcard templates be used during enrollment to help reduce end-point detection errors?
   These templates are introduced in (Holmes & Holmes, §8.10, p.123), and their use in training is duscussed in §8.13 on pp.125-6. In essence the silence template allows for gaps and pauses in a recording, and the wildcard can be used to represent parts of a training utterance that are being captured.

4. What human organ produces quasi-periodic source of voiced sounds, such as vowels?
   Vocal folds (aka. vocal cords) which are in the larynx.
5. What is fundamental frequency (also called f₀), and how is it produced?
   It is the frequency that separates the pitch harmonics in the spectrum and is usually the frequency of the lowest harmonic peak. The periodic vibration is the result of oscillation of the vocal folds, in the larynx.
6. The vocal tract comprises three main passages. The pharynx and oral cavity are two. What is the third?
   Nasal cavity.
7. The velum, larynx and jaw cooperate in the production of speech. Name two other articulators.
   Lips and tongue (body or tip).
8. What is a formant and how is it produced?
   A frequency region of high amplitude in a speech spectrum or spectrogram which is produced as the result of an acoustic resonance in the vocal tract.

9. What is the name of the organ in the inner ear that is responsible for converting physical vibrations into a set of nerve responses (i.e., electrical signals)?
   Cochlea.
10. What is the bandwidth to which the human ear responds (to one significant figure), and what are the implications?
    20 kHz, which implies a sampling rate above 40 kHz for hi-fi quality.
11. If I calculate a DFT directly from a 40ms section of a speech signal, what will be the spacing of frequency bins in the spectrum?
    25 Hz.
12. Boxcar (rectangular), Kaiser and Blackman define certain kinds of window. Name three other popular window functions.
    Hann, Hamming, Bartlett (triangular), Tukey, Gaussian, etc.
13. What would be an appropriate window size for a narrow-band spectrogram?
    Choosing 40 Hz between adjacent bins implies a minimum 25 ms window, typically it is at least 30 ms.
14. Give an estimate of the SNR for a full-scale 16-bit speech signal in relation to the quanisation noise.
    Signal uses 2¹⁶ peak-to-peak, the noise is 2⁰=1 (+/- half a bit), which gives a range of 96 dB (=16×6 dB).

Given an initial state vector π = [0.25 0.50 0.25], and state-transition probability matrix A = [0.25 0.50 0.25; 0.00 0.25 0.50; 0.00 0.00 0.25]: draw the model to show the states and permissible transitions; See figure S1 opposite. calculate the probability of the state sequence X = {1, 2, 2, 3} The product of the initial-state prob and subsequent transition probs is: P(X={1,2,2,3}|M) = ¼ × ½ × ¼ × ¼ × ¾ = 3/512, which includes the transition to the exit node.   Using the Markov model presented in the lectures, if today has been rainy, what is the most likely weather tomorrow, It's most likely to rain, since P(x2=1|x1=1) = 0.4; meanwhile P(x2=2|x1=1) = P(x2=3|x1=1) = 0.3.   in two days' time (i.e., on Wednesday)? It turns out most likely to be sunny: P(x3=3|x1=1) = (0.4×0.3)+(0.3×0.2)+(0.3×0.8) = 0.42; whereas P(x3=1|x1=1) = 0.25 and P(x3=2|x1=1) = 0.33.   Calculate the probabilities of rain-rain-sun, rain-cloud-sun and rain-sun-sun, assuming πrain = 1. P(X={1,1,3}|x1=1,M) = 0.12, P(X={1,2,3}|x1=1,M) = 0.06, P(X={1,3,3}|x1=1,M) = 0.24,   Hence, if we are told that it will be sunny on Wednesday for certain and that it's rainy today, what's the most likely weather tomorrow? Well, it looks like it's going to be sunny tomorrow too!

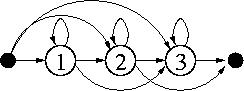
Fig.S1. State transitions.

Considering the state-transition topologies shown in Figure 2: write an expression for the state duration probability P(τ|λ) in Fig.2(a); P(τ|λ) = (aii)τ-1 (1-aii) = 0.9τ-1×0.1   write an expression for the duration probability for each state P(τ|x=i,λ) in Fig.2(b); P(τ1|λ) = 0.8τ1-1×0.2 P(τ2|λ) = 0.6τ2-1×0.4   hence derive the distribution of duration probabilities for the entire model in Fig.2(b); P(τ=τ1+τ2|λ) = P(τ1|λ) * P(τ1|λ), where * denotes convolution. Hence, P(τ|λ) = {0, 0.2×0.4×Σν=0..τ-2 0.8τ-2-ν 0.6ν, ...} =>  P(τ|λ) = {0, 0.08, 0.112 0.1184, 0.112, 0.0896, ...}   how many terms are there in this expression for the model duration with τ=5? There are four terms, which correspond to the state sequences {1,1,1,1,2}, {1,1,1,2,2}, {1,1,2,2,2} and {1,2,2,2,2}.

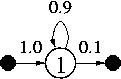(a)   (b) 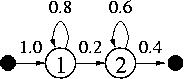  Fig.2. HMM state transitions.

6. How can a bank of band-pass filters (each tuned to a different centre frequency) be used to extract a feature vector that describes the overall spectral shape of an acoustic signal at any particular time?
   A vector can be made up by taking the energy in each band, averaged over a short period (e.g., 20 ms).
7. The real cepstrum of a digital signal sampled at 48 kHz is defined as c_s(m) = IDFT( ln|S(k)| ), where S(k) is the signal's discrete Fourier spectrum, ln|.| denotes the natural logarithm and IDFT is the inverse discrete Fourier transform. Considering only real, symmetric elements in the log-magnitude spectrum (i.e., the cos terms), draw the shapes of the first four cepstral coefficients c₀, c₁, c₂ and c₃, in the log-magnitude spectral domain.
   These are respectively a constant and three cosine functions of the form cos x, cos 2x and cos 3x.
8. What properties of the Mel-frequency cepstrum make it more like human auditory processing, compared to the real cepstrum?
   The warping of the frequency axis, based on human pitch perception.
9. In calculating MFCCs, what is the purpose of:
   1. the log operation;
      compression, source-filter decomposition
   2. mel-frequency binning;
      perceptual weighting of information
   3. Discrete Cosine Transform?
      make coefficients independent, diagonalising their covariance

Draw a trellis diagram for the HMM in Fig.2(b) and a 5-frame observation sequence. Show all the paths that arrive in the final null node after the fifth frame. See Figure S2.   How many different paths are there for this model and number of observations? Four, just as there were four terms in the answer to Q.5d above (week 3).   Imagine you are designing an optical character recognition (OCR) system for converting images of written words into text, based on HMMs. The observations you're given come in the form of pixellated grey-scale bitmaps of a single line of writing. Explain in general terms how you would construct the following components of the system: frames of feature vectors to make up the observation sequences; Either parameterise each column of pixels as a feature vector, or register the locations of the individual characters and produce a vector from the extracted bitmap.   the models (each one comprising a state or set of states); Either model each character as a sequence of pixel columns, or as one character observation. Could include some context-sensitive models for handwriting strokes, or for special printed characters, e.g., "fi" and "fl" compared to a standard "f".   suitable annotations to be used during training; A transcript of the text, including blanks and blotches where encountered.   any special models (e.g., for dealing with blotches or blank spaces within the pictures). A blank space model and a generic blotch model could be supplemented by models for any unusual characters (e.g., footnote, trademark and copyright symbols, mathematical symbols or phonetic alphabet). A model for lines could be considered, but it might be better to try to eliminate them in the pre-processing stage.   How do the components of the OCR system compare to those for an ASR system designed to perform an Isolated Word Recognition task? Pretty well! The same components are required for an IWR system: (a) sequences of acoustic feature vectors, (b) models with multiple states for to represent the sequence of sounds produced in each vocabulary word, (c) transcriptions of the utterances, and (d) silence and wildcard models.

(a)   (b)   Fig.2. HMM state transitions. 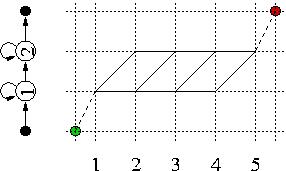     Fig.S2. Trellis diagram for τ=5.

1. In the Viterbi algorithm, what is the purpose of the variable ψ_t(i)?
   Indicator of the best predecessor, which can then be used during traceback to identify the best path.
    
2. What is the meaning of Δ^*?
   The total likelihood of the best path, the joint probability of the observations and the optimal state sequence given a particular model P(O,X^*|λ).
    
3. Using the Viterbi algorithm, calculate the path likelihoods δ_t(i), the value of Δ^*, and use the values of ψ_t(i) to extract the best path X^*. Model parameters: π=[1 0], A=[0.8 0.2; 0.0 0.6], η=[0 0.4]^T, and B=[0.5 0.2 0.3; 0.0 0.9 0.1] where the columns of the B matrix correspond to green (G), blue (B) and red (R) events, respectively.
   1. for observations O¹={G,B,B} (worked example from lecture)
      

      Step 1.	δ1(1) =	1×0.5 = 0.5	ψ1(1) = 0
      	δ1(2) =	0	ψ1(2) = 0
      Step 2.	δ2(1) =	0.5×0.8×0.2 = 0.08	ψ2(1) = 1
      	δ2(2) =	0.5×0.2×0.9 = 0.09	ψ2(2) = 1
      	δ3(1) =	0.08×0.8×0.2 = 0.0128	ψ3(1) = 1
      	δ3(2) =	max[0.08×0.2, 0.09×0.6] × 0.9 =0.054×0.9 = 0.0486	ψ3(2) = 2
      Step 3.	Δ* =	max[0.0128×0, 0.0486×0.4] = 0.01944	x3* = 2
      Step 4.	x2* =	ψ3(x3*) = ψ3(2) = 2
      	x1* =	ψ2(x2*) = ψ2(2) = 1	X*¹={1,2,2}

      
       
   2. for observations O²={R,B}
      

      Step 1.	δ1(1) =	1×0.3 = 0.3	ψ1(1) = 0
      	δ1(2) =	0	ψ1(2) = 0
      Step 2.	δ2(1) =	0.3×0.8×0.2 = 0.048	ψ2(1) = 1
      	δ2(2) =	0.3×0.2×0.9 = 0.054	ψ2(2) = 1
      Step 3.	Δ* =	max[0.048×0, 0.054×0.4] = 0.0216	x2* = 2
      Step 4.	x1* =	ψ2(x2*) = ψ2(2) = 1	X*²={1,2}

      
       
4. What is the difference between the cumulative likelihoods α_t(i) computed in the forward procedure, and those δ_t(i) computed in the Viterbi algorithm?
   The probability α_t(i)=P(o₁^t, x_t=i|λ) is based on all possible paths leading to the current node; whereas δ_t(i)=P(o₁^t, x₁^t-1, x_t=i|λ) is based only on the best path upto and including the current state i.
    
5. Floating-point variables with double precision (i.e., 4 bytes) can store values down to 1e-308, typical state-transition probs are in the order of 0.1, and the multi-dimensional output probability would be around 0.01 for a good match.
   1. Given these approximations and assuming no re-scaling of the probabilities, state at what stage would it become impossible to compare competing hypotheses (i.e., different paths through the trellis)? In other words, after how many observations would you expect the likelihoods to suffer from numerical underflow?
      So, we need to find the value of T for which (1e-3)^T=1e-308.
      T=log(1e-308)/log(1e-3) = 103, or ∼100 observations.
       
   2. With an observation frame rate of 10 ms, roughly how long would this take?
      1 second.
       
6. Instead of storing the likelihoods directly as in the previous question, we choose to store them as negative log probabilities using a 16-bit unsigned integer (quantising each decade into 32 levels).
   1. How many decades (factors of ten) can we represent with this data type?
      65536/32 = 2048 decades.
       
   2. How many seconds of observations (at 10 ms) could we now process before suffering from underflow?
      2048/(3×100) = 6.83 s, or ∼7 seconds.

[week 6 solutions]

Week 8

[homework solutions]