| |
Slow space and time modulation of the small-amplitude
travelling periodic waves bifurcating from the neutral curve
in fluid mechanics, such as two-dimensional plane Poiseuille flow,
leads to a complex Ginzburg-Landau model equation, typically of
the form shown to the right where A(x,t) is complex valued.
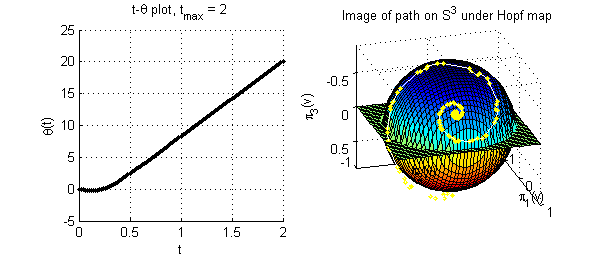
A class of solitary wave solutions is the Hocking-Stewartson
pulse (HS pulse). The linear stability problem for
the HS pulse can be reduced to a complex four-dimensional ODE,
and the exterior algebra formulation gives a six-dimensional ODE.
A Hopf bundle, with total space the 11-dimensional sphere and
1-sphere fibre, is constructed and the linear stability problem is
integrated on this bundle. The Matlab codes for this integration
are given below.
|


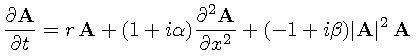

 Hopf bundle homepage
Mathematics homepage
Hopf bundle homepage
Mathematics homepage
